【例題】

13²-(14-x)²=15²-x²

単に答えを求めるだけなら、次のように両辺を展開して、整理して解を求めればいいでしょう。

13²-(14-x)²=15²-x²
169-(196-28x+x²)=225-x²
169-196+28x-x²=225-x²
-27+28x-x²=225-x²
28x=252
x=9

ただ、計算量が多くなり複雑です。
そこで、a²-b²=(a+b)(a-b)と因数分解の公式を利用して計算すると少し簡単に求めることができます。

13²-(14-x)²=15²-x²
x²-(14-x)²=15²-13²
{x+(14-x)}{x-(14-x)}=(15+13)(15-13)
14×(2x-14)=28×2
2x-14=4
2x=18
x=9

速く正確に計算するためには、このような工夫が必要なのです。

【例題】

大小2つのサイコロを1回ふり,大のサイコロの出た目をa,小のサイコロの出た目をbとするとき,2a+3bが５の倍数になる確率を求めなさい。

a=1 のとき,2a+3bが5の倍数になるbの値はb=1,6
a=2 のとき,2a+3bが5の倍数になるbの値はb=2
a=3 のとき,2a+3bが5の倍数になるbの値はb=3
a=4 のとき,2a+3bが5の倍数になるbの値はb=4
a=5 のとき,2a+3bが5の倍数になるbの値はb=5
a=6 のとき,2a+3bが5の倍数になるbの値はb=1,6

したがって求める確率は、 836 = 29 になります。

上記のように書き出して確率を求めることが必要になります。

ただ、効率よく正確に数え上げるためには、次のような表を書いて数え上げたほうが数え漏れなどのミスは少なくなります。

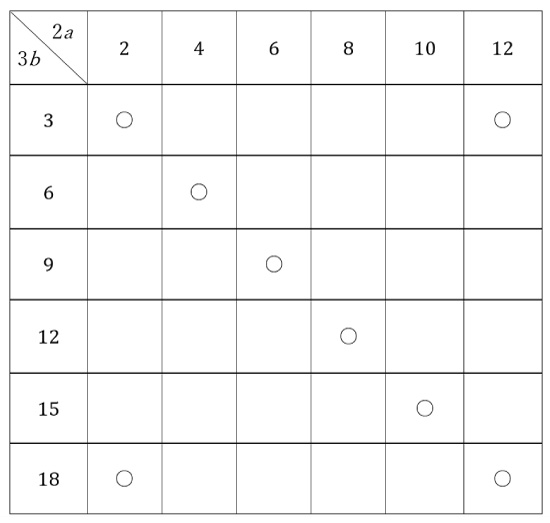
このように計算や作業に関しては、常に時間を意識し、工夫して楽な方法を模索する姿勢が必要です。
馬渕教室では、中１～中３まで継続的に計算のトレーニングを行い、神戸総理の入試に必要な高い計算力をみにつけていくとともに、解法にこだわった指導を行います。

【例題】

A君はP地点を午前10時に出発して、15Km離れたQ地点まで、時速12kmの速さで向かった。A君のお父さんは午前10時45分にQ地点をミニバイクに乗って出発して、時速20kmの速さでP地点に向かった。
このとき、お父さんがQ地点に向かう途中、A君とすれちがったのは、P地点から何kmの地点か求めなさい

＜考え方＞
速さの文章題です。このような問題は、2人の動きをグラフ(ダイヤグラム)で表して、2人の進行の状況を把握すると解法の方針がたてやすくなります。

A君とお父さんのダイヤグラムをかくと、下のようになります。
それぞれのグラフの交点がお父さんとA君が出会った場所になります。

したがって

を解くと、x= 2554 、y= 454

よって、 454 km…【答】

少し手順も計算量も多いですね。
次のように図形的な性質を利用して解くとどうでしょうか。

上のダイヤグラムにおいて、黒く塗られた三角形どうしは相似です。
相似比は、90：30＝3：1ですから、P地点からPQ間の距離を3：1に分けた地点で出会っていることがわかります。

よって、15× 34 = 454 km…【答】

相似を利用した方が、計算量も少なく素早く簡単に解くことができますね。
神戸総理のような問題構成ではこういった素早い解法が必要になります。

馬渕教室の「平日授業・神戸総理専門クラス」「日曜特訓・神戸総理専門クラス」では、良問を厳選したオリジナルのテキストを通して、単元別演習を行い、神戸総理の入試に必要な解法パターンを効率よく確実に習得していきます。